史密斯夫妇邀请另外四对夫妇就餐,已知他们每个人都不和自己握手,不和自己的配偶握手,且不和同一个人握手一次以上。在大家见面握手寒暄后,史密斯问大家握手了几次,每个人的答案都不一样。
问:史密斯太太握手几次?
【解析】
解决本题可用排除法,把一些无关的信息先予以排除,可以确定的问题先确定,尽可能缩小未知的范围,以便于问题的分析和解决。这种思维方式在我们的工作和生活中都是很有用处的。根据已给的条件可知:
(1)总共10个人,每个人不与自己握手,不与配偶握手,不与同一个人握手超过一次,所以每个人最多握8次手,最少0次。
(2)史密斯先生问其他9个人握了几次手,各人回答不一样,所以每个人的握手次数应为0-8次,每种不同次数有1个人。可知除了斯密斯先生外,其他九个人的握手次数如图1所示。
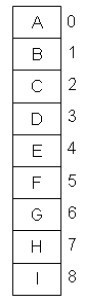
图1 四对夫妇及史密斯夫人的握手次数
假设I握了8次手,即I与其配偶以外的所有人都握了手;可以假设I为史密斯太太,她握了八次手,即与史密斯先生以外的每个人都握了一次手。可以推知除斯密斯夫妇外的其他三对夫妇的握手次数至少为1,与上面推断已知的A的握手次数为0冲突。所以假设不成立。并可推知握手0次的A和握手8次的I为一对夫妇。实际的握手情况按夫妻分配可以参考图2:
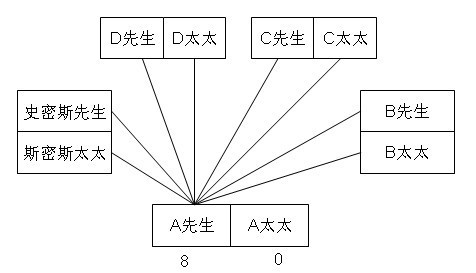
图2 五对夫妇中一对夫妇的握手情况
(3)根据(2)可知A夫妇其中一人,与每个人握手一次,另外一个人没有握手。所以可以排除夫妇A,即假设夫妇A没有参加聚会,其余七人的握手次数减1,此时参加聚会的人数为史密斯夫妇和另外三对夫妻8人。除史密斯先生外,其他7人的握手次数情况如图3所示。
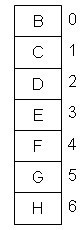
图3 三对夫妇及史密斯夫人的握手次数
假设H为史密斯太太,则斯密斯太太与其他三对夫妇每人握手一次,即其他6人的握手次数至少为1次,但是根据图3可知,B握手0次,所以假设不成立,即H不是史密斯太太,并可推知B和H是一对夫妇。去掉夫妇A后握手情况按夫妻分配可以参考图4:
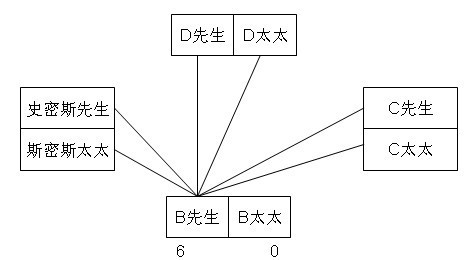
图4 四对夫妇中一对夫妇的握手情况
(4)去掉夫妇B后(即假设夫妇B没有参加聚会)其余五人的握手次数分配情况如下图5所示。
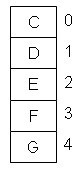
图5 两对夫妇及史密斯夫人的握手次数
假设G为史密斯太太,则斯密斯太太与其他两对夫妇每人握手一次,即其他4人的握手次数至少为1次,但是根据图5可知,C握手0次,所以假设不成立,即G不是史密斯太太,并可推知C和G是一对夫妇。去掉夫妇B后握手情况按夫妻分配可以参考图6:
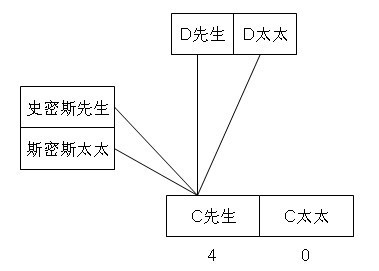
图6 三对夫妇中一对夫妇的握手情况
(5)去掉夫妇C后(即假设夫妇C没有参加聚会)其余三人的握手次数分配情况如图7所示。
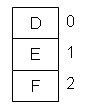
图7 一对夫妇及史密斯夫人的握手次数
假设F为史密斯太太,则斯密斯太太与另外一对夫妇每人握手一次,这2人的握手次数至少为1次,但是根据图7可知,D握手0次,所以假设不成立,即F不是史密斯太太,并可推知D和F是一对夫妇。去掉夫妇B后握手情况按夫妻分配可以参考图6:
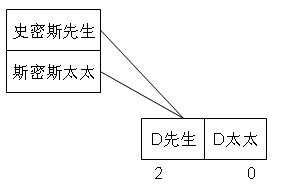
图8 两对夫妇中一对夫妇的握手情况
而剩下的E便是史密斯太太。根据图1可知她总共握了四次手。
【答案】
史密斯夫人握了四次手。
说明:查找这9个人中谁是史密斯太太,和查找这9个人中谁不是史密斯太太的结果是一样的。这就是排除法的实现技巧。





This is just a random comment. The former practice in many elementary schools of beginning the detailed study of American history without any previous knowledge of general history limited the pupil’s range of vision, restricted his sympathies, and left him without material for comparisons.