已知每架飞机有一个油箱,飞机之间可以相互加油,一个整油箱的油可以供一架飞机绕地球飞行半圈。为使至少一架飞机绕地球一圈回到飞机起飞的机场,至少需要使用几架飞机,飞行几个架次?
注意:所有飞机从同一飞机场起飞,而且必须安全返回机场,不允许中途降落,一架飞机起飞一次算作一架次,加油时间可以忽略。
【分析】
借助于图形解决问题的方法就是图形法。根据问题中已知的条件,采用适当的方法画出图形,有助于问题的解决。有些问题,在没画图之前,会觉得无从下手,画了图后就一目了然了。
对于本题只是用脑子去想象来解决这道题是件很复杂的事,如果借助于图形来解决就简单多了。在此假设地球的长度为1,根据题意可知一油箱的油可以让一架飞机绕地球持续飞行1/2。现假设飞机起飞地点为x,如图1所示。
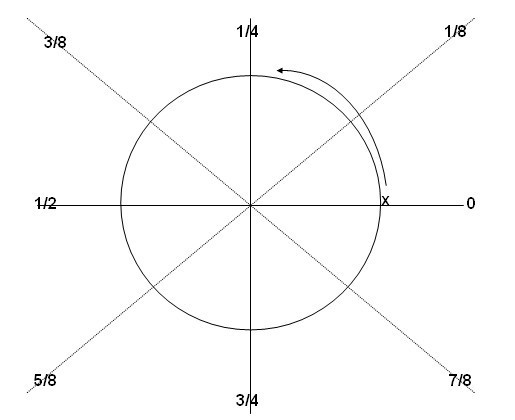
图1 飞机环行地球示意图
根据条件可推知,只用一架飞机肯定是无法完成任务的。当用两架飞机时,两架飞机的油量刚好够一架飞机绕地球一圈,无论怎么补充也完成不了航行任务。所以至少有三架飞机,设为飞机A,飞机B和飞机C。整个飞行过程如下:
(1)三架飞机同时从飞机场x同向起飞。如图2所示。
(2)到1/8时A、B和C的可持航油量都为3/8,此时C将油量的1/8给B,另外1/8的油量给A后,A和B的剩余可持航油量1/2,C剩余1/8的可持航油量正好足够返航。A、B继续飞行,C返航。如图3所示。
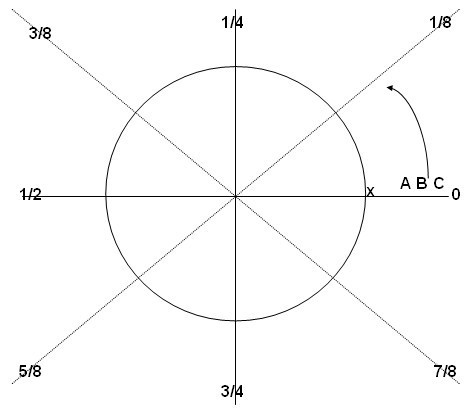
图2 三架飞机同时逆时针起航
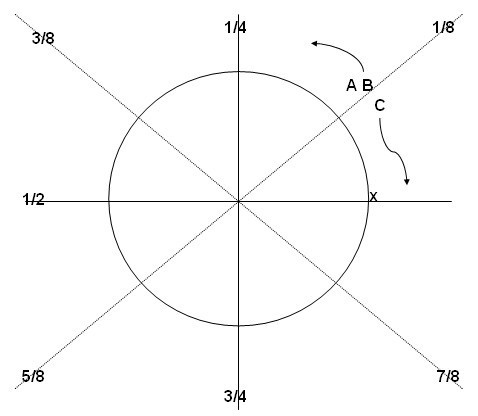
图3 C返航
(3)到达1/4处时A和B的可持航油量都为3/8,C已返回机场。此时B将1/8的油量给A,A的可持航油量为1/2,B的可持航油量为1/4恰好可以安全返航,此时A继续绕地球飞行,B返航,如图4所示。
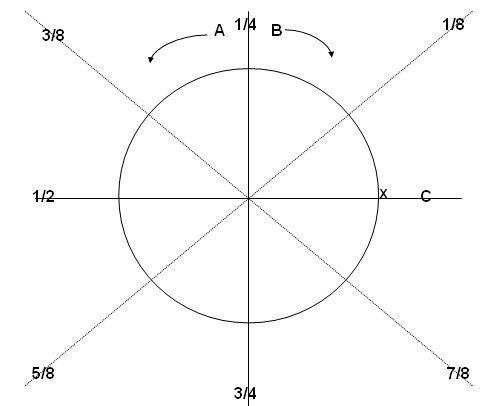
图4 B返航
(4)当A到达1/2处时,A的可持航油量为1/4,此时A继续绕地球飞行。B已经到达机场,B加满油顺时针起飞,如图5所示。
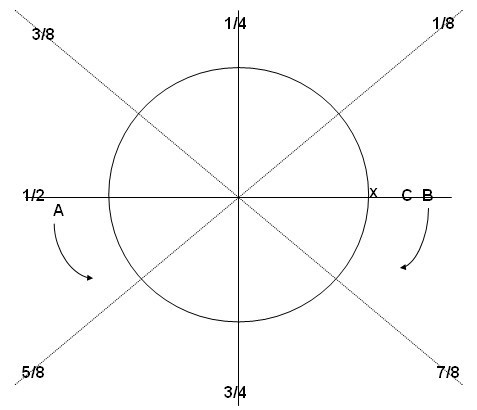
图5 B顺时针起航
(5)A和B在3/4处相遇,此时A的可持航油量为0,B的可持航油量为1/4,B将1/8的可持航油量分给A后,A、B的油量相等,都为1/8。A和B同时逆时针飞行,C此时在机场装满油顺时针起飞。如图6所示。
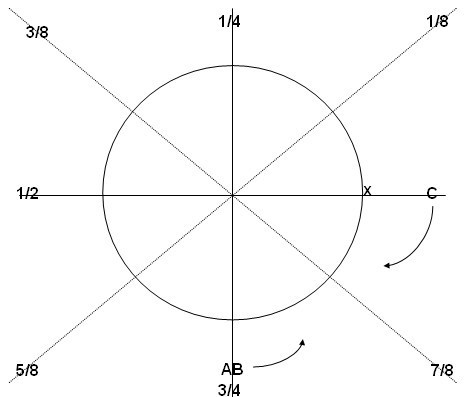
图6 C顺时针起航,B逆时针返航
(6)A、B和C相遇在7/8处,此时A和B的油量为0,C的油量为1/4,C将1/8的可持航油量分给A,再将1/8的可持航油量分给B后,三者的油量相同,都恰好够飞回机场。三架飞机逆时针向机场飞行。如图7所示。
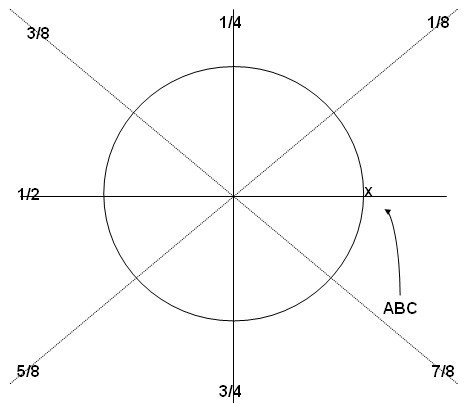
图7 C逆时针返航
(7)三架飞机同时安全返回机场,飞机A成功绕地球飞行一圈。
共用了三架飞机,A起飞一次,B起飞两次,C起飞两次。所以共用了三架飞机,5个航次。
注意:根据观察可以发现后1/2的飞行情况是前1/2的反序。所以在分析完前1/2时,就已经可以算出总共需要的飞机架次。
【答案】
共用了三架飞机,5个航次。
说明:事实上,许多问题都要运用几种不同的方法才能解决。所谓综合法,就是综合各种方法(包括前述各种方法以外的方法)去解决某些问题。所以不要只是简单的硬套方法,应该了解各种方法的技巧,随机应变。





This is just a random comment. The former practice in many elementary schools of beginning the detailed study of American history without any previous knowledge of general history limited the pupil’s range of vision, restricted his sympathies, and left him without material for comparisons.