假设排列着100个乒乓球,由两个人轮流拿球装入口袋,能拿到第100个乒乓球的人为胜利者。
条件是:每次拿球者至少要拿1个,但最多不能超过5个。
问:如果你是最先拿球的人,你该拿几个?以后怎么拿就能保证你能得到第100个乒乓球?
【分析】
怎么样才能保证自己能拿到最后一个呢,最简单的方法就是最后剩6个,该对方来拿,这样他最多拿5个,要剩下第100号,至少拿1个,那样的话剩下的5就全归自己了当然也包括第100号了。
(1)控制每一轮拿出的个数。
要控制每次两个人取出的个数,两个人最多拿10个,但是每次对方拿的个数是不受控制的,假设对方拿n个,自己可以拿6-n个,这样两个人的每次拿的数量就是6个。(为什么自己要拿6-n呢?因为对手最多拿5个时,这时自己最少能拿一个,和就是6个,自己不能把数值控制的更低。而对手最少拿1个时,自己最多拿5个,和就是6个,自己不能把数值控制的更高。因此只有6才是一个自己可控的数值。 (2)自己拿第一次拿x,以后每一次自己和对方拿出的个数都是6,一次循环下去,最多拿到第15轮,就是自己和对手共拿出了15 * 6+x个。还剩10-x个,此时该对方拿,应该保证剩下6个,自己才能拿到100,所以x应该为4。
过程如图1所示。
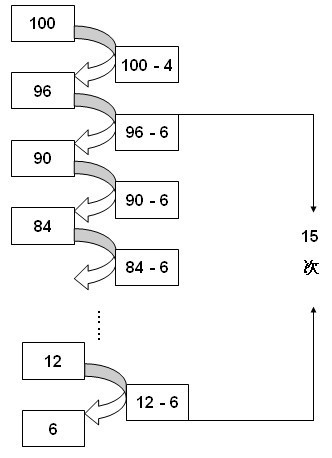
图1 成功拿取第100号球过程
【答案】
第一次拿4个,以后每轮对方拿n个球后,自己拿6-n个球。15轮后剩下6个球,该对方先拿,对方拿后剩余的自己全拿,就可以拿到100号球了。
说明:倒推法是本题的关键,根据最后结果得出解题方法。在很多时候,倒推法是解题的唯一思路,但是一定要确保能够知道最后结果,才可使用这种方法。





This is just a random comment. The former practice in many elementary schools of beginning the detailed study of American history without any previous knowledge of general history limited the pupil’s range of vision, restricted his sympathies, and left him without material for comparisons.